Background

What is the most important part of an FRC team? There are so many key aspects that there is no single answer. However, most people would agree that the driver(s) plays a vital role in a team’s success. It is essential that the driver is able to control his/her robot with maximum precision. This can not be stressed enough. What can we do with software to aid the driver?

Often overlooked yet glaringly obvious is also what is right in your hands: the controller joysticks.

Manipulating joystick inputs effectively can:

  • Prevent driver overshoot

  • Enhance micro-adjustment accuracy and control

  • Customize the ‘feel’ for the user

Deadzones

Every controller is an imperfect device. Due to hardware imperfections, when a joystick returns to the neutral position, the joystick does not usually map to exactly 0.0 input. So, it is common to have a ‘deadzone’ (also called a ‘deadband’), where any input less than the deadzone is mapped to zero. Here is some naive pseudocode with a 20% deadzone:

1double user_input = controller.getRightX();
2
3if(user_input < 0.2){
4    user_input = 0;
5}

If graphed with the input on the \(x\) axis and the output on the \(y\) axis:


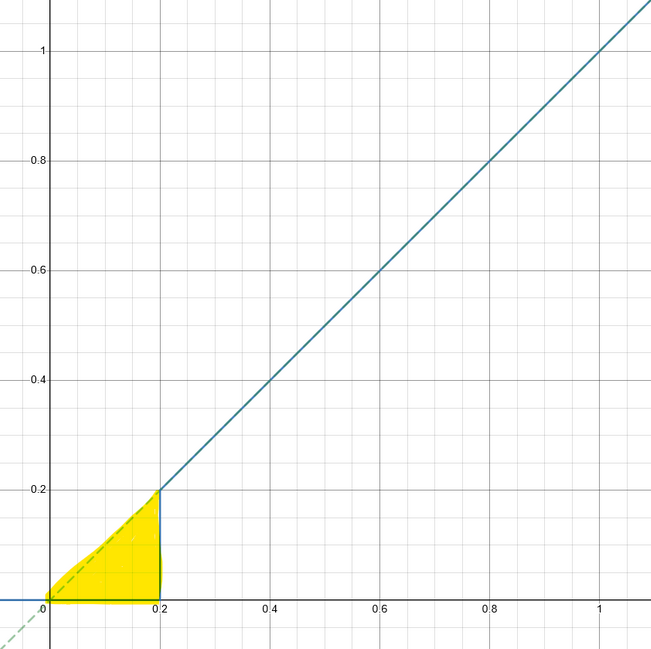
Deadzone


The area highlighted in yellow is the input where precision control is lost. This poses an issue; the user is limited to a minimum input of 20%! If used for the drivetrain, this will lead to driver overshoot; for other controls, it inhibits the user’s ability to make fine precision adjustments critical for game-piece acquisition or scoring opportunities.

One could object:

“A 20% deadzone is very large! A more typical deadzone is 5%.”

Even with a small deadzone, it is always preferred to offer the user maximum flexibility if the performance cost is small. In reality, we need a better algorithm.

What we really want is something more like this:


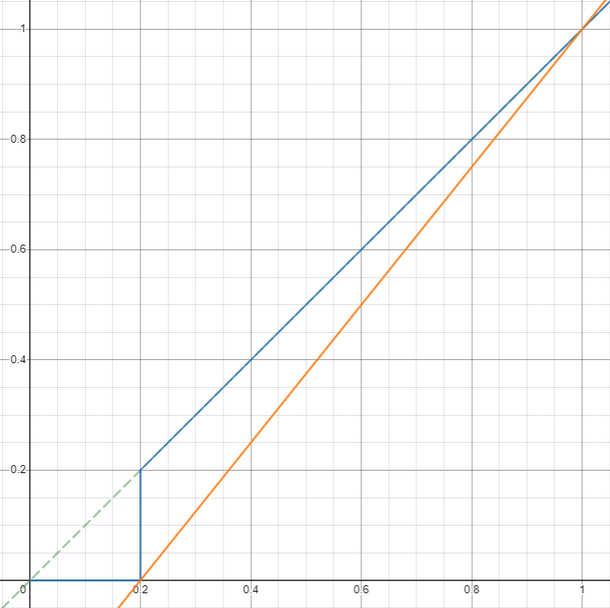
Mapped Deadzone


That’s much better. The orange line, a linear interpolation of the blue line, is the more intuitive deadzone characteristic. With some range checking, we can apply a deadzone without sacrificing precision.

Response Curves

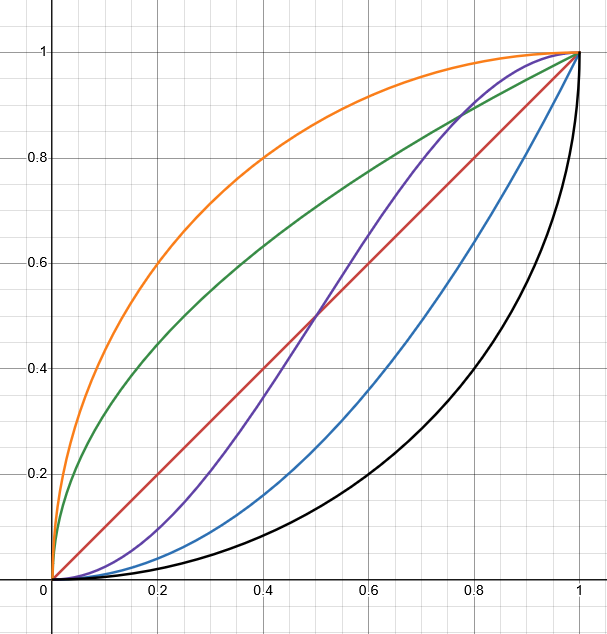
Response curves are functions that will transform the input in a non-linear fashion. allowing one to customize the ‘feel’ of a joystick. Some example response curves are shown below with the input on the \(x\) axis and the output on the \(y\):


Curve

🟥 \(y = x\)

🟦 \(y = x^2\)

🟩 \(y = \sqrt{x}\)

⬛ \(y = 1-\sqrt{1-x^{2}}\)

🟧 \(y = \sqrt{1-\left(x\ -1\right)^{2}}\)

🟪 \(y = \frac{1\cos\left(\pi\left(x+1\right)\right)}{2}\ +\ \frac{1}{2}\)

Response Curves

A response curve in combination with a deadzone is very effective in customizing and normalizing joystick feel.

The most applicable response curves for drivetrains are generally exponential (e.g. \(x^n\) where \(n \geq 1\)) because they reduce input on the low end, allowing a user to more easily make micro-adjustments, and accelerate the input towards the high end, so that maximum output is not inhibited. However, programmers should ponder their own use case; an alternative function may be preferable.